 Search Here
Search Here
MISC
Parts List
Robot Forum
Chat
Member Pages
Axon MCU
Robot Books
Shop
Contact
SKILLS
How To Build
A Robot
Tutorial
Calculators
Mechanics
Programming
Miscellaneous
Robots
Space
HARDWARE
Actuators
Batteries
Electronics
Materials
Microcontrollers
Sensors
SCIENCE
Robot Journals
Robot Theory
Conferences

|
No good robot can ever be built without gears. As such, a good understanding of how gears affect parameters such as torque and velocity are very important. In this tutorial I will first talk about the basics of gears, how to use them properly along with simple equations, and then I will go into specific types of gears.
As with all motors, by looking at the motor datasheet you can determine the output velocity
and torque of your motor. But unfortunately for robots, motors commercially available do
not normally have a desirable speed to torque ratio (the main exception being
servos and high torque motors with built in gearboxes).
For example, do you really want your robot
wheels to rotate at 10,000 rpm at low torques? In robotics, torque is better than speed.
With gears, you will exchange the high velocity with a better torque.
This exchange happens with a very simple equation that you can calculate:
Torque_Old * Velocity_Old = Torque_New * Velocity_New
Torque_Old and Velocity_Old can be found simply by looking up the datasheet of your motor.
Then what you need to do is put a desired torque or velocity on the right hand side of the equation.
My statics and dynamics
tutorials can help you decide on a reasonable torque and/or velocity for your robot.
So for example, suppose your motor outputs 3 lb-in torque at 2000rps according to the datasheet, but you only want 300rps.
This is what your equation will look like:
3 lb-in * 2000rps = Torque_New * 300rps
With highschool algebra you can then determine that your new torque will be 20 lb-in.
Now suppose, with the same motor, you need 5 lb-in (minimum force to crush a cat, obviously). But suppose you also need 1500rps minimum velocity.
How would you know if the motor is up to spec and can do this? Easy . . .
3 lb-in * 2000rps = 5 lb-in * Velocity_New
Velocity_New = 1200rps
You now have just determined that at 1200 rps the selected motor is not up to spec.
Using the simple equation, you have just saved yourself tons of money on a motor that would have never worked.
Designing your robot, and doing all the necessary equations beforehand, will always save you tons of money and time.
The gearing ratio is the value at which you change your velocity and torque. Again, it has a very simple equation.
The gearing ratio is just a fraction which you multiple your velocity and torque by.
Suppose your gearing ratio is 3/1. This would mean you would multiple your torque by 3 and your velocity by the inverse,
or 1/3.
example; Torque_Old = 10 lb-in, Velocity_Old = 100rps
Achieving a Particular Gearing Ratio
For a much more accurate way to calculate the gearing ratio, calculate the ratio of teeth on the gears.
If one gear has 28 teeth and the other
has 13, you would have a (28/13=2.15 or 13/28=.46) 2.15 or .46 gearing ratio. I will go into this later,
but this is why worm gears have such high gearing ratios. In a worm gear setup, one gear always has
a single tooth, while the other has many - a guaranteed huge ratio. Counting teeth will always give you the
most exact ratio.
For example, suppose you use two spur gears, you would typically expect efficiency to be around ~90%.
To calculate, multiply that number by your Velocity_New and Torque_New to get your true output velocity and torque.
if (from above example)
then
effienciency_total = gear_type_efficiency ^ (# of gears - 1) = .9 ^ (29) = 4.7 %
If instead you used 5 gears, you would have:
effienciency_total = .9 ^ (4) = 65.6 %
It is easy to figure out that if they are on the same shaft, the velocity (rotations per second) is the exact same.
To calculate torque, you must use the moment arm balance equations from my
statics tutorial. In this case, the radius is the moment arm.
radius_gear1 * torque_gear1 = radius_gear2 * torque_gear2
In this example, what minimum torque does the motor need to pull the weight up?
writing down the equations:
simplifying, we get:
so therefore the minimum required motor torque is
Now what if you wanted the weight to lift at 2 feet/sec. What rotations per second and direction must the motor rotate at?
writing down the equations:
simplifying, we get:
so therefore the required motor rps is
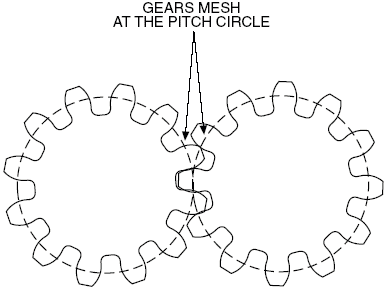
The pitch diameter is as shown. To calculate the pitch, simply use this equation:
Pitch = # teeth / pitch circle diameter (in inches)
For example, a gear with 72 teeth and a 1.5" pitch diameter is 48 Pitch.
Gears that mesh must both have the same pitch and pressure angle (usually 20 degrees).
Note: The efficiencies listed are only typical. Because of many other factors could be present,
the listed efficiencies should only be used as a guide. Often manufacturers will give you expected
efficiencies in the datasheets for their gears. Remember, wear and lubrication will also dramatically
affect gear efficiencies.
More Information
Mechanical Advantage, Torque vs. Rotational Velocity
Gears work on the principle of mechanical advantage. This means that by using different gear diameters,
you can exchange between rotational (or translation) velocity and torque.

Gearing Ratios
I have done the equations, but how do you mechanically swap torque and velocity?
You would use two gears (sometimes more) of different diameters to have a particular gearing ratio.
In any pair of gears, the larger gear will move more slowly than the smaller gear, but it will move
with more torque. Thus, the bigger the size difference (or gearing ratio) between two gears, the
greater the difference in speed and torque.
Gearing ratio = 2/3
Torque * 2/3 = 6.7 lb-in
Velocity * 3/2 = 150rps

If you wanted a simple gearing ratio of say 2 to 1, you would use two gears, one being twice as big as the other.
It isn't really the size as much as the diameter ratio of the two gears.
If the diameter of one gear is 3 times bigger than the other gear, you would
get a 3/1 (or 1/3) gearing ratio. You can easily figure out the ratio by hand measuring the diameter of
the gears you are using.
Gear Efficiency
Unfortunately, by using gears, you lower your input to output power efficiency. This is due to obvious things
such as friction,
misalignment of pressure angles, lubrication, gear backlash (spacing between meshed gear teeth between two gears)
and angular momentum, etc.
Different gear setups, different types of gears,
different gear materials, and wear and tear on the gear, will all have different efficiencies. The possible
combinations are too big to list, so I will give you an estimated efficiency to expect with
each gear type below. You can also find a much more exact efficiency by looking
up the datasheet on the gears you are using.
Gearing ratio = 2/3
Torque * 2/3 = 6.7 lb-in
Velocity * 3/2 = 150rps
true torque = 6.7 * .9 = 6 lb-in
true velocity = 150 * .9 = 135rps

Direction of Gear Rotation
When designing your gear setup you should understand how gearing changes the rotation direction of your output.
Two gears touching will always be counter rotation, meaning if one rotates clockwise, the other will always
rotate counterclockwise. Obvious, I know. But what if you have a chain of say 6 gears touching? The rule is, an
odd numbers of gears always rotates in the same direction, and even numbers of gears are counter-rotational.
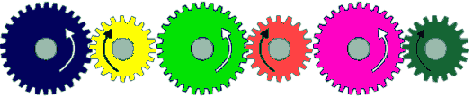
Gear Chains (more than 2 gears together)
Suppose you have 30 gears (holy squirrels!), all in order, like in the image above. How in the monkies do you
calculate the gearing ratio of that behemoth? Easy. Ignore all the gears in between the very first and very last gear.
If the diameter of the first gear is 2 inches, and the diameter of the last is 1 inch, you have a 2:1 ratio.
The gears in between do not matter. Now what direction does the last gear rotate?
Easy, you have an even number of gears, so it is counter-rotational of the first gear. What
efficiency do you have? Well thats:
Compound Gears
A compound gear is where you have two gears fixed on the same shaft.

torque_motor * radius_gear1 = torque_gear2 * radius_gear2
torque_gear2 * radius_gear2 = torque_gear3 * radius_gear3
torque_gear3 * radius_gear3 = weight * radius_gear3
torque_motor * radius_gear1 = weight * radius_gear3
torque_motor = weight * radius_gear3 / radius_gear1
rps_motor * radius_gear1 = rps_gear2 * radius_gear2
rps_gear2 = rps_gear3
rps_gear3 * 2*pi*radius_gear3 = velocity_weight
rps_motor * radius_gear1 = rps_gear3 * radius_gear2
or
rps_motor * radius_gear1 = velocity_weight / (2*pi*radius_gear3) * radius_gear2
rps_motor = 2 ft/sec * radius_gear2 / (2*pi*radius_gear3 * radius_gear1)
Gear Pitch
When selecting your gears, the three most important numbers you must know are
pitch, pitch diameter, and number of teeth.
Gear Types
All gears, no matter the type, work on the same principles above. However the different types let you
accomplish different things. Some types of gears have high efficiencies, or high gearing ratios, or
work at different angles, for example. Below are the main common types. This is not a complete list.
It is also possible to have a combination in types.
Spur Gears (~90% efficiency)

Spur gears are the most commonly used gears due to their simplicity and the fact that they have
the highest possible efficiency of all gear types. Not recommend for very high loads as
gear teeth can break more easily.
Helical Gears (~80% efficiency)

Helical gears operate just like spur gears, but offer smoother operation.
You can also optionally operate them at an angle, too. Unfortunately,
due to the complex shape, they are generally more expensive.
Sproket Gears With Chains (~80% efficiency)
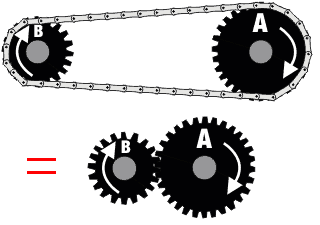
Two gears with a chain can be considered as three separate gears. Since there is
an odd number, the rotation direction is the same. They operate basically like
spur gears, but due to increased contact area there is increased friction (hence
lower efficiency). Lubrication is highly recommended.
To change the length of any chain, you will need what is called a chain breaker.
This is a cheap device you can buy at any bike store. It helps in removing and placing
pins within the chain.
Bevel Gears (~70% efficiency)

Bevel gears are good for changing the rotation angle. Unfortunately they suffer
low efficiencies, so avoid use if possible.
Rack and Pinion (~90% efficiency)
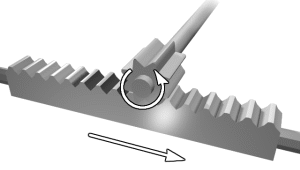
Rack and Pinion is the type of gearing found in steering systems. This gearing
is great if you want to convert rotational motion into translational. Mathematically,
use radius = 1 for the straight 'gear'.
Worm Gears (~70% efficiency)

Worm gears have a very high gearing ratio. To mathematically calculate, consider
the worm gear as a single tooth. Another advantage to the worm gear is that it
is not back-drivable. What this means is only your motor can rotate the main gear,
so things like gravity or counter forces will not cause any rotation. This is good say
if you have a robot arm holding something heavy, and you don't want to waste power on holding torque.
The efficiency is low, but lubrication really helps.
Planetary Gears (~80% efficiency)
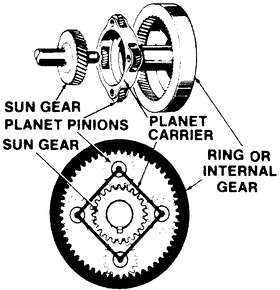
Planetary gears have the highest commercially available gear ratios you would ever want to put
on a robot. But since they are somewhat complicated, you would never need to build one, just use it.
The datasheet should tell you the gearing ratio - I just wanted you to know if you need a really
really high gearing ratio for a robot, planetary gears are the way to go. Even better, some planetary
gears offer multiple gearing ratio's that are user configurable!
If you wish for an even more in-depth tutorial about gear selection, you can find it in this
advanced gear selection tutorial.
I didn't write it, but it's easy to follow and understand. Where can you buy gears? Check my
robot parts list and the ad window at the top right of this page
for links.
Society of Robots copyright 2005-2014