 Search Here
Search Here
MISC
Parts List
Robot Forum
Chat
Member Pages
Axon MCU
Robot Books
Shop
Contact
SKILLS
How To Build
A Robot
Tutorial
Calculators
Mechanics
Programming
Miscellaneous
Robots
Space
HARDWARE
Actuators
Batteries
Electronics
Materials
Microcontrollers
Sensors
SCIENCE
Robot Journals
Robot Theory
Conferences
|
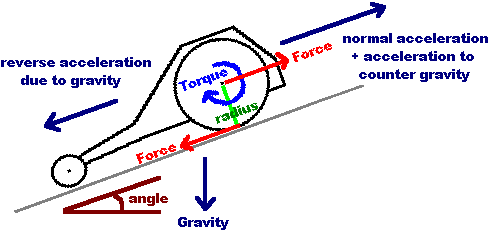
While statics is the study of structures at a fixed point in time, dynamics is the study of structures over a period of time. Basically statics studies things that dont move, while dynamics studies things that do. Statics is concerned with moments, forces, stresses, torque, pressure, etc. Dynamics is concerned with displacement, velocity, acceleration, momentum, etc. If you want to calculate and/or optimize forces generated or required for a moving robot, this tutorial has the basics that you will need to understand. It is highly recommended you read the statics tutorial first as this tutorial will build off of it.
Displacement and Velocity
We all know what velocity is, but how do you design a robot to go at a defined velocity?
Of course you can put a really fast motor
on your robot and hope that it will go fast enough.
But if you can calculate it you can design it to go your required speed without doubt, and leave the rest
of the motor force for torque.
So how to do this? For an example, suppose you have a wheeled robot that you want to run over
old people with. You know from experiments that old people can run at 3 feet per second. So what
motor rpm do you need, and what diameter should your wheels be, so they cant get away or hide their
medicine?

Conceptually, every time your wheel rotates an entire revolution, your robot travels the distance equal to the circumference of the wheel. So multiply the circumference by the number of rotations per minute, and you then get the distance your robot travels in a minute.
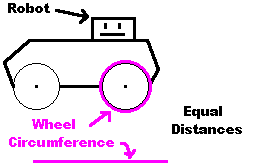
Velocity = circumference * rpm
Velocity = diameter * pi * rpm OR Velocity = 2 * radius * pi * rpm
For example, if your motor has a rotation speed (under load) of 100rpm (determined by looking up the motor part number online) and you want to travel at 3 feet per second, calculate:
3 ft/s = diameter * pi * 100rpm
3 ft/s = diameter * pi * 1.67rps (rotations per second)
diameter = 3 ft/s / (3.14 * 1.67 rps)
diameter = 0.57 ft, or 6.89"
Torque = Distance * Force
Robot Wheel Diameter vs Torque
You probably noticed that the larger the diameter of the wheel, or higher the rpm, the faster your robot will go.
But this isn't entirely true in that there is another factor involved.
If your robot requires more torque than it can give, it will go slower
than you calculated. Heavier robots will go slower. Now what you need to do is compare the motor torque,
your robot acceleration, and wheel diameter. These three attributes will have to be
balanced to achieve proper torque.
Motor Torque and Force
High force is required to push other robots around, or to go up hills and rough terrain, or have high
acceleration. As calculatable with statics, just by knowing your
wheel diameter and motor torque, you can determine the force your robot is capable of.
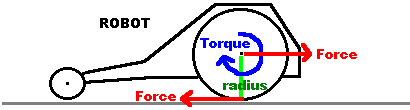
Distance = Wheel Radius
Force = Torque / Wheel Radius

|
Check out the user friendly RMF Calculator, or my outdated excel sheet for calculating RMF. |
1) To use this equation, look up a set of motors you think will work for your robot and write down the torque and rps (rotations per second) for each.
2) Then multiply the two numbers together for each. This will be your robot motor factor.
3) Next, estimate the weight of your robot. Basically add up the weight of all the parts.
4) Lastly, choose your desired velocity and acceleration.
5) Compare both sides of the equation
Example. Suppose you found three motors:
Motor A: 2 lb ft, 1rps => RMF = 2 lb ft rps
Motor B: 2.5 lb ft, 2rps => RMF = 5 lb ft rps
Motor C: 2 lb ft, 4rps => RMF = 8 lb ft rps
Now suppose you want a velocity of 3 ft/s, an acceleration of 2 ft/s^2, and you estimate your robot weight to be 5 lbs.
so RMF >= 5 lbs * 2 ft/s^2 * 3 ft/s / (2 * pi)
therefore RMF >= 4.77 lb * ft * rps
So this means you need a motor with an RMF greater or equal to 4.77. Looking at your list, Motor B and C both will work. However Motor C is probably overkill, so it's just a waste of money. Therefore you would use Motor B. Just note that if none of the motors would work, you would have to either reduce weight, or go slower, or find another motor.
note: if you convert rps to radians/sec, RMF can be measured in watts
Calculating Wheel Diameter
So now what robot wheel diameter should you use?
Going back to an earlier equation,
velocity = diameter * pi * rps
3 ft/s / (pi * 2/s) = wheel diameter = .48 feet = 5.73"
OR
diameter = velocity / (pi * rps)
You are finished! You use motor B, with a wheel diameter of 5.73", and never again will your robot fail at plowing over the neighborhood cat.
Although the above equations are intended for robot wheels, they will also work for any other robot part. If you were say designing a robot arm, instead of using diameter use robot arm length. Then you can calculate how fast the arm will move with a certain weight being carried, for example.
Robot Motor Factor, Efficiency
The RMF you calculated is only for a 100% efficient system. But in reality this never happens.
Gearing and
friction and many other factors cause inefficiency.
I won't go into how to calculate efficiency, but there are general rules that would get you really close.
If you have external (not inside the motor) gearing, reduce your efficiency by ~15%. If you
are using treads like on a tank robot, reduce by another ~30%. If your robot operates on
rough high friction terrain, reduce another ~10%. For example, a tank robot on rough terrain
would have an efficiency of (100% - 30%)*(100% - 10%) = 63% or 0.63.
The RMF equation, incorporating efficiency, is
Torque * rps > = Mass * Acceleration * Velocity * (1/efficiency) / (2 * pi)
where efficiency is a percentage expressed as a decimal number (i.e. 80% = .8).

|
Again, check out the user friendly RMF Calculator, or my outdated excel sheet for calculating RMF. |
Society of Robots copyright 2005-2014